CF 2039D
Description
Solution
當 $i=1,\; \forall j \in [2,n] :$ $$a_{\gcd(1,j)}=a_1 \neq \gcd(a_1,a_j)$$ 觀察得到 $$a_1 \neq \gcd(a_1,a_j) \iff a_1 \nmid a_j$$
先假設 $a_1$ 滿足 $a_1 \nmid a_j$ ,繼續往下推。
當 $i=2,\; \forall j \in [3,n] :$ \[ a_{\gcd(2,j)} = \begin{cases} a_1 \neq \gcd(a_2, a_j), & j \text{ is odd.} \\ a_2 \neq \gcd(a_2, a_j), & j \text{ is even.} \end{cases} \]
- 當 $j$ 是奇數:因為前面已經假設 $a_1$ 不會整除其他數,它自然也不會是其他兩數的最大公因數,所以這條式子成立。
- 當 $j$ 是偶數:同樣可得 $a_2 \neq \gcd(a_2,a_j) \iff a_2 \nmid a_j$ 。
接著再假設 $a_2 \nmid a_j$ ,推 $i=3,\;\forall j \in [4,n]$ 的情況,這樣不斷推下去可以得到一個結論: $$\forall\, i \in [1,n],\;\forall\, j \in (i,n],\;\forall\, k \in [2,\left\lfloor \frac{n}{i} \right\rfloor] \quad a_i\neq \gcd(a_i,a_j) \iff a_i \nmid a_{ki}$$
結論有了,怎麼構造? 其實很簡單,一個數不能整除比他小的數,題目又剛好要求字典序最大,因此考慮以下構造方式:
- 令題目給定的集合 $S = \{ s_1, s_2, \dots, s_m \}, \quad s_1 < s_2 < \cdots < s_m$
- $a_1=s_m$
- 對於 $i \geq 2$ ,令 \(a_j = \min \{ a_k \mid k \text{ divides } i \land k \neq i \}\) 。若 $a_j$ 為 $s_t$, 則令 $a_i$ 為 $s_{t-1}$ ;若 $t=1$ 則無解。
時間複雜度 $O(n \log n)$ 。
CF 2112D
Description
Solution
觀察
- $n = 2$ 無解
- $u \rightarrow v \rightarrow w$ 有 $3$ 個 good pair
- $v_1\rightarrow v_2 \leftarrow v_3 \rightarrow \dots \leftarrow v_k$ 有 $k-1$ 個 good pair
找到一個度數為 $2$ 的節點 $v$ ,假設 $v$ 相鄰的節點為 $v, w$ ,就像觀察二一樣構造 $u \rightarrow v \rightarrow w$ ,剩下的點就像觀察三一樣接上去就好,參考下圖
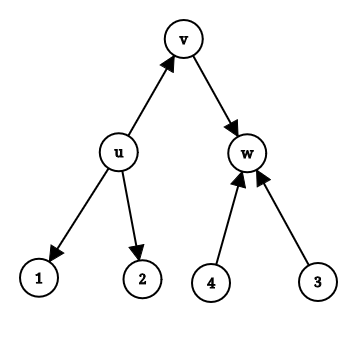
時間複雜度 $O(n)$ 。
CF 1975D
Description
Solution
觀察
- $P_A,\,P_B$ 亂逛是沒有用的,應該先找到最先被染色成藍色的點,假設為 $v$ 。
- 假設所有的點中與 $v$ 的最遠距離為 $d$ ,答案為 $dis(b, v) + 2(n-1) - d$ 。
時間複雜度 $O(n)$ 。
CF 1430D
Description
Solution
對於操作一,先從由單一字元構成且長度 $\geq 2$ 的子字串開始刪,且由左往右,如果找不到這種子字串則從最左邊開始刪。
時間複雜度 $O(n)$ 。
CF 1777C
Description
Solution
觀察
- 因為 $\{1,\,2,\,\cdots,\, \frac{m}{2}\}$ 中的每一個數必定至少是 $\{\frac{m}{2}+1,\,\frac{m}{2}+2,\,\cdots ,\,m\}$ 其中的一個因數,因此只需要檢查 $\left[\frac{m}{2}+1, m\right]$ 。
- 重複的元素沒有用。
根據觀察可以把數列 $a$ 中所有小於 $(\frac{m}{2}+1)$ 的數與重複的數刪掉,排序後使用雙指標,檢查當前的數是不是 $\left[\frac{m}{2}+1, m\right]$ 之中的倍數,若小於就跳出迴圈,否則不斷右移直到能湊齊 $\left[\frac{m}{2}+1, m\right]$ 。
最糟的情況是 $m = n$ ,根據觀察可以把數列的長度縮減成最多 $\frac{n}{2}$ 且裡面元素不重複,所以檢查所有數是不是 $\left[\frac{m}{2}+1, m\right]$ 之中的倍數的總次數是 $1 + 2 + \dots + \frac{n}{2} \approx \frac{n^2}{8}$ 。
時間複雜度 $O(n^2)$ 。